|
Функции |
| void | BesselExe (TOptics InOptics, TOptics OutOptics, TModes Modes, unsigned short Param) |
| | ДОЭ обеспечивающий построение мод бесселевого пучка.
|
| void | NullBessel1D (TComplex1D out, TModes Modes, unsigned short Param) |
| void | BesselNonParaxialFresnelTransformExe (TOptics InOptics, TOptics OutOptics, TModes Modes, unsigned short Param, double lamda, double z) |
| | Непараксиальный бесселевый пучок прошедший расстояние z.
|
| void | BesselParaxialFresnelTransformExe (TOptics InOptics, TOptics OutOptics, TModes Modes, unsigned short Param, double lamda, double z) |
| | Параксиальный бесселевый пучок прошедший расстояние z.
|
| void | BesselNonParaxialFresnelImagingExe (TOptics InOptics, TOptics OutOptics, TModes Modes, unsigned short Param, double lamda, double a, double z) |
| | Идеальный бесселевый пучок, прошедший через линзу.
|
| void | FastKirhgof2Exe (TOptics InOptics, TOptics OutOptics, int ExpCount, bool RadialDevelopment, double lamda, double z) |
| | Распространение светового поля на любые расстояния.
|
| void | Kirhgof2Exe (TOptics InOptics, TOptics OutOptics, int ExpCount, double lamda, double z) |
| | Распространение светового поля на любые расстояния.
|
| void | FastKirhgof2UnilateralExe (TOptics InOptics, TOptics OutOptics, int ExpCount, bool RadialDevelopment, double lamda, double z, int OutX, int OutY) |
| | Распространение светового поля на любые расстояния.
|
| void | ThinLensExe (TOptics InOptics, TOptics OutOptics, double lamda, double f) |
| | Преобразование тонкой линзы.
|
| void | ThickLensExe (TOptics InOptics, TOptics OutOptics, double lambda, double n, double delta, double R1, double R2) |
| | Преобразование толстой линзы.
|
| double | SKO (TOptics TestOptics, TOptics StandardOptics) |
| | Получение среднеквадратичного отклонения (СКО).
|
| void | FastFourier (TOptics InOptics, TOptics OutOptics, int zeros, double lamda, double f) |
| | Оптическое преобразование Фурье через быстрое дискретное.
|
| void | Fourier (TOptics InOptics, TOptics OutOptics, double lamda, double f) |
| | Оптическое преобразование Фурье через быстрое дискретное.
|
| void | fftFrenel (TOptics InOptics, TOptics OutOptics, int zeros, double lamda, double z) |
| | Оптическое преобразование Френеля через БПФ.
|
| void | Frenel (TOptics InOptics, TOptics OutOptics, double lamda, double z) |
| | Оптическое преобразование Френеля в интегральном исполнении.
|
| void | FrenelUnilateral (TOptics InOptics, TOptics OutOptics, double lamda, double z, int OutX, int OutY) |
| | Оптическое преобразование Френеля в интегральном исполнении.
|
| void | hankelFrenel2D (TComplex1D InOptics, TOptics OutOptics, double lamda, double z, int m) |
| | Оптическое преобразование Френеля через Ханкеля для однмодового 1D распределения.
|
| void | hankelFrenel1D (TComplex1D InOptics, TComplex1D OutOptics, double lamda, double z, int m) |
| | Оптическое преобразование Френеля через Ханкеля для однмодового 1D распределения.
|
| void | hankelFourier2D (TComplex1D InOptics, TOptics OutOptics, double lamda, double f, int m) |
| | Оптическое преобразование Фурье через Ханкеля для однмодового 1D распределения.
|
| void | Diafragma (TOptics InOptics, TOptics OutOptics, double DiafragmaX, double DiafragmaY) |
| | Оптическое преобразование Диафрагмы.
|
| void | FastDiafragma (TOptics InOptics, TOptics OutOptics, double DiafragmaX, double DiafragmaY) |
| | Ускоренное оптическое преобразование Диафрагмы.
|
| double | Energy (TOptics Optics) |
| | Получение энергии сосредоточеной в оптическом поле.
|
| void | hankelFourier1D (TComplex1D InOptics, TComplex1D OutOptics, double lamda, double f, int m) |
| | Преобразование Ханкеля и производные.
|
![\[ U(\rho , \varphi , z)= \sum_{\alpha , n} J_n(\alpha \rho) \exp (in \varphi), \]](form_9.png)
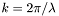 - волновое число,
- волновое число, 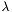 - длинна волны светового поля.
- длинна волны светового поля. 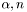 - параметры мод.
- параметры мод. 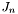 . - построение пучка с функцией
. - построение пучка с функцией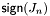
![\[ U(\rho , \varphi , z)= \sum_{\alpha , n=0} \frac{a}{z} \exp \left[ i \frac{k \rho ^2}{2z} \left( 1 + \frac{a}{z} \right) \right] J_0 \left( \frac{\alpha \rho a}{z} \right) \exp (in \varphi), \]](form_17.png)
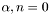 - параметры мод.
- параметры мод. ![\[ U(\rho , \varphi , z)= \sum_{\alpha , n} \exp \left[ -i \frac{z \alpha ^2}{2k} \right] J_n(\alpha \rho) \exp (in \varphi), \]](form_14.png)
![\[ U(\rho , \varphi , z)= \sum_{\alpha , n} (-i)^{n+1} \sqrt{\frac{\rho_0}{2 \pi}} \frac{k}{z} \exp \left[ i \frac{k}{2z} (\rho ^2 + \rho_0^2)\right] J_n \left( \frac{k\rho \rho_0}{z} \right) \exp (in \varphi), \]](form_15.png)
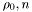 - параметры мод.
- параметры мод. 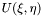 ].
]. 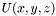 ].
]. ![\[ U(x,y,z)= - \frac{z} {2\pi} \int\int_{D} U(\xi ,\eta)\frac{e^{ikr}} {r^2} \left(ik-\frac{1}{r} \right) d\xi d\eta , \]](form_19.png)
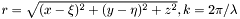 - волновое число,
- волновое число, ![\[ U(x,y,z)= \frac{k e^{ikz} } {2 \pi z i} \exp \left( \frac{ik(x^2 + y^2)} {2z} \right) W\left[ U(\xi , \eta) \exp \left( \frac{ik( \xi ^2 + \eta ^2 )} {2z} \right) \right], \]](form_29.png)
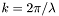 - волновое число,
- волновое число, 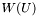 - БПФ.
- БПФ. ![\[ U(x,y,f)= \frac{k} {f} \int\int_{D} U(\xi , \eta) \exp \left[ -ik \frac{ik(x \xi + y \eta )} {f} \right] d\xi d\eta , \]](form_27.png)
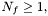 где
где 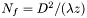 - число Френеля, где
- число Френеля, где 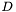 - диаметр пучка. В противных случаях используют преобразование Фурье (
- диаметр пучка. В противных случаях используют преобразование Фурье (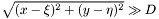 , в противном случае используется преобразование Кирхгофа (
, в противном случае используется преобразование Кирхгофа (![\[ U(x,y,z)= \frac{k} {2 \pi z i} \int\int_{D} U(\xi , \eta) \exp \left( \frac{ik} {2z} \left[ (x-\xi)^2 + (y-\eta)^2 \right] \right) d\xi d\eta , \]](form_35.png)
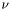 функции
функции 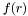 является выражение:
является выражение: ![\[ F_\nu(k) = \int_0^\infty f(r)J_\nu(kr)\,r\,dr \]](form_44.png)
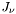 является
является 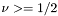 . Обратное преобразование Ханкеля
. Обратное преобразование Ханкеля 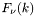 известно как выражение:
известно как выражение: ![\[ f(r) =\int_0^\infty F_\nu(k)J_\nu(kr) k~dk \]](form_48.png)
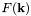 в зависимости от радиус-вектора
в зависимости от радиус-вектора 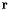 . Это преобразование Фурье выглядит так:
. Это преобразование Фурье выглядит так: ![\[ F(\mathbf{k})=\frac{1}{2\pi}\int\int f(\mathbf{r}) e^{-i\mathbf{k}\cdot\mathbf{r}}\,d\mathbf{r} \]](form_51.png)
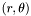 оставляя тот же вектор
оставляя тот же вектор 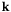 для оси
для оси 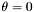 . Преобразование Фурье в данной полярной системе координат примет вид:
. Преобразование Фурье в данной полярной системе координат примет вид: ![\[ F(\mathbf{k}) = \frac{1}{2\pi}\int_{r=0}^{\infty}\int_{\theta=0}^{2\pi}f(r,\theta)e^{-ikr\cos(\theta)}\,r\,dr\,d\theta \]](form_55.png)
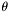 является углом между векторами
является углом между векторами 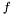 является радиально симметричной, она не должна зависеть от угла
является радиально симметричной, она не должна зависеть от угла ![\[ F(\mathbf{k})=F(k)= \int_0^\infty f(r) J_0(kr) r\,dr \]](form_58.png)
![\[ f(r, \phi)= R(r) \exp(i m \phi) . \]](form_36.png)
![\[ F(u,v,f)=\frac{k}{f} \int\int f(x,y) \exp \left[ - \frac{ik}{f}(xu + yv) \right] \,dx,dy \]](form_40.png)
![\[ F_m(\rho,\theta,f) = 2\pi \exp(i m \theta) \frac{k}{f} \int_0^\infty R(r) J_m \left( \frac{k r \rho} {f} \right) r\,dr \]](form_41.png)
![\[ F_m(\rho,\theta,z) = \exp(i m \theta) \frac{k} {z} \frac{k} {2 \pi z i}\exp(ikz) \exp \left( \frac{i k \rho^2} {2 z} \right) \int^{\infty}_{0} R(r) \exp \left( \frac{i k r^2} {2 z} \right) J_m \left( \frac{i k r \rho} {z} \right) r dr , \]](form_37.png)
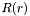 ].
]. 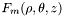 ].
]. ![\[ \delta= \sqrt{ \frac{\int\int_{D}(|U_{std}(x,y,z)| -|U_{tst}(x,y,z)|)^2dxdy} {\int\int_{D}|U_{std}(x,y,z)|^2dxdy} } \]](form_24.png)
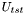 ).
). 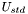 ).
). ![\[ U(x,y,f)= U(\xi ,\eta) \exp \left[-\frac{ik}{2f} (\xi ^2 + \eta ^2)\right] , \]](form_23.png)
